Δ-Σ ADC由Δ-Σ调制器和数字滤波器构成。调制器将模拟输入转换为数字比特流,而数字滤波器将比特流转换为表示模拟输入幅度的数据字。
让我们来看看调制器是如何工作的,首先从一阶Δ-Σ调制器拓扑结构的基本分析开始,如图1所示。
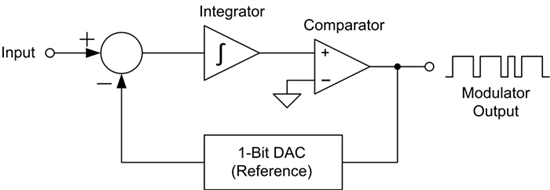
图 1:Δ-Σ调制器内部框图
调制器根据调制器时钟运行,决定了输入的采样间隔。调制循环通过对输入采样和1位DAC之间的差分进行积分而开始。
比较器根据积分器值确定下一个调制器输出。根据比较器的输出状态,1位DAC产生与ADC的正或负基准电压相等的电压。如果调制器输出为1,则从输入中减去基准电压。如果调制器输出为0,则在输入中加上基准电压。在每个调制器时钟脉冲,调制器完成一个完整的周期并产生一个新的输出。
当调制器时钟继续运行时,每个调制器时钟脉冲将产生另一个调制器输出脉冲。所得到的输出比特流成为与基准电压成比例的输入电压的另一种表示。图2显示了输入正弦波和得到的调制器输出比特流,假设基准电压为1V。
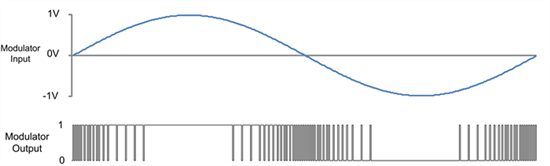
图 2:正弦波输入(上图)和调制输出比特流(下图)
当输入接近1V时,调制器的比特流的1s密度接近100%。相反,当输入接近-1V时,比特流1s密度接近0%。当输入为0V时,1s密度为50%。因此,可以在不超出调制器范围的情况下测量基准电压和负基准电压之间的输入电压。
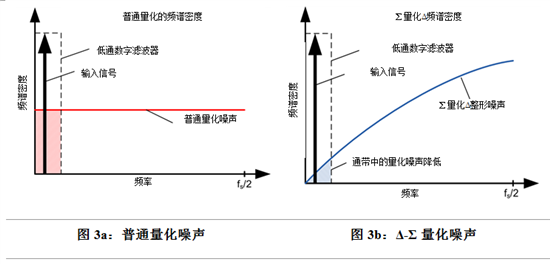
那么通过将输入转换为比特流调制器实现了什么?观察调制器的频谱内,输入电压和采样数字信号之间的误差被建模为量化噪声,如图3a所示。采用二了简单的量化,误差频谱密度是从DC到采样频率(fS)的白噪声除以2。
通过使用Δ-Σ调制,量化误差频谱密度被调至更高的频率,如图3b所示。低通数字滤波器保留具有较高分辨率的输入信号,因为量化噪声已经移动到数字滤波器的通带之外。使用Δ-Σ调制,我们减少了量化噪声,实现了更高的分辨率。
具有额外前馈和反馈路径的多阶的不同调制器拓扑结构可以提供比上述基本示例更好的噪声整形。不同的数字滤波器提取原始信号,以更高的测量分辨率加速ADC。
通过将这种复杂的拓扑结构分解到基本水平,您可以看到Δ-Σ调制器的工作原理:调制器对输入信号进行采样,将其与基准进行比较,输出与基准相比与输入信号的幅度成比例的1s的比特流。请留意下个月的Precision Hub模拟精密技术杂谈,届时我将讨论如何结合调制器和数字滤波器以获得更大的测量分辨率。
有关更多详细信息,请参阅以下资源:
查看TI丰富的delta-sigma ADC。
delta-sigma ADC的工作原理,第一篇,作者:Bonnie Baker,模拟应用期刊
delta-sigma ADC的工作原理,第二篇,作者:Bonnie Baker,模拟应用期刊
观看delta-sigma ADC在低功率称重应用中的视频演示。
原文链接: