作者:Kevin Duke
我们的 DAC 基础知识系列文章现已涵盖大量的技术信息,从简单的理想数模转换器 (DAC) 到减少干扰等复杂问题,应有尽有。在本系列的最后一篇文章中,我们将讨论总体未调整误差 (TUE)。
高精度 DAC 可实现出色的 DC 性能或极低频率性能。在很多高精度 DAC 应用中,与代码转换、干扰和压摆率有关的 AC 误差技术参数在定义 DAC 精确度时可以忽略。这是因为输出在大部分时间里是趋稳不变的。
在《DAC 基础知识:静态规范与线性度》一文中,我介绍了所有 DAC DC 误差参数:失调误差、零代码误差、增益误差、差分非线性 (DNL) 与积分非线性 (INL)。在试图表达 DAC 在 DC 下有多精确时,很难考虑到所有这些误差源。这正是 TUE 的亮点所在。它是一个对所有这些误差源进行综合后得出的单个数字,用以简洁表达 DC DAC 输出的精确度。唯一的不足是需要您做一点统计工作。
在统计过程中,可使用名为和的平方根 (RSS) 的方法来为误差分析累计不相关的误差源。在串形和梯形 DAC 架构中,失调、增益和 INL 误差来自 DAC 架构的不同组成部分。这就意味着它们是不相关的,可安全使用 RSS 技术。计算公式如下:
您可能已经注意到了,我并没有列入零代码误差和 DNL。这是因为零代码误差只适合很小部分的 DAC 输出。对于 16 位 DAC 来说,这可能是 65,536 个总代码中的几百个代码。同时,DNL 事实上已通过 INL 纳入误差计算。
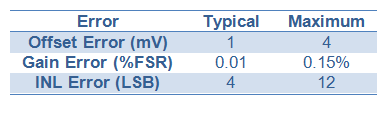
现在,我们来看一个简短的实例,了解如何计算 TUE。下面是 16 位双通道 DAC8562 说明书中的最大和典型技术参数。
DAC8562 的每个技术参数都采用不同的单位提供,这是行业标准。要计算 TUE,每个参数都要采用相同的单位,因此我们将使用下表转换各值。
在单位转换完成后,我们可将这些值带回 TUE 公式,并计算 DAC8562 的总体未调整误差。
使用所有技术参数的最大值,可得到我所指的、+/-111 LSB、+/-8.5mV 或 0.17% FSR 的“可能最大 TUE”。我之所以这样说是因为产品说明书中的最大值是 3-∑ 数字,应该包含曾经产生的所有部分的 99.7%。在典型的高斯分布中,这些边缘情况不太可能发生。您更不可能找到所有参数都表现出最大误差(“绝对最大误差”,就是简单将所有误差加到一起得到的数字)的器件。即便是该“可能最大 TUE”,也是个不太可能观察到的单位。
使用典型数字,可得到您将从大部分系统中看到的最真实估值。DAC8562 的典型TUE 是 +/- 23 LSB、1.78mV 或 0.0356% FSR。查看这款德州仪器 (TI) 高精度设计在真实系统中的真实数据,了解该方法的实际使用及业经验证的可靠性。
记住,这些参数还具有与其相关的方向性问题。对于具有正失调误差的 DAC 来说,负增益误差实际上有助于让系统更准确。在使用 RSS 累计最大误差时,这点未纳入考虑范围内。因此在很多情况下,对典型误差数字进行 RSS 计算,仍然只能得到很一般的 TUE 估值。