作者:Captain Luo
SVPWM,即空间矢量脉宽调制,由于在相同直流母线电压下的电压利用率比SPWM(正弦脉宽调制)高约15%,因而被广泛应用于电机伺服驱动以及变频器等场合。然而,传统的SVPWM算法实现需要判断矢量的扇区位置并计算矢量作用时间,求解过程设计较多浮点、三角函数与除法等运算,这对于低成本的微控制器而言,其运算难度较大。因此,设计一种运算简单,易于微机实现的改进SVPWM算法具有重要意义。典型的电机矢量控制框图如下:
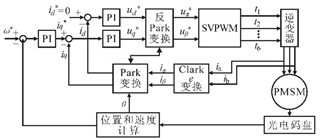
图1 矢量控制框图
可见SVPWM部分的目的就是把输入的 , 转换成六个开关管的导通时间,对应电机需要的ABC三相绕组电压。通过数字方式实现矢量控制时,往往以占空比(实际为微机中用于产生PWM的比较值)代替实际电压值。因此,在实现SVPWM时,仅需处理相应的坐标变换即可。
按电机绕组为星形连接为例,传统SVPWM按照8种开关状态进行分区,是基于六扇区进行矢量的分解与计算的,实际上(110,101,011)均可由(100,010,001)两两合成,即可简化为三扇区。如下图所示:
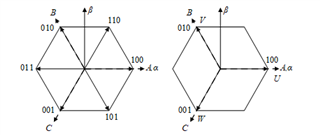
图2 六扇区与三扇区
为与电机相轴区分,将(100,010,001)三电压矢量方向分别称为U、V和W轴。由于 , 是比较值形式的,将其坐标变换至UVW轴后将直接是每相上桥臂的占空比(比较值)。由于平面矢量合成仅需两个线性无关的基本矢量,因此只需在UVW三轴中任意选择两个作为一个基,这里选取UV两轴。
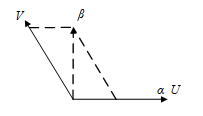
图3 矢量分解图
αβ轴到UV轴的矢量分解图如上图所示,其满足平行四边形法则,由图有
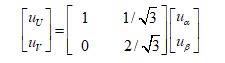 (1)
(1)
根据UV轴坐标的正负与大小关系,可将平面分为三个扇区,如图3所示,图中“+”号表示值为正数,“-”号则表示值为负数,在W轴线上有U=V。
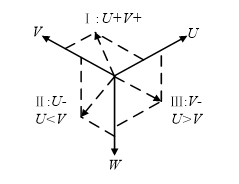
图4 扇区划分
前面提到,UVW轴坐标将直接是每相上桥臂的占空比(比较值),而在实际微机中比较值不能是负数,因此当UV中坐标出现负值时,可通过轴间对称性等效转换为另外两轴的正坐标。以SVPWM的五段法为例,即零矢量全部为000矢量,其三相占空比(比较值)TA、TB与TC表达式如表3-2所示。
表1 各扇区占空比算式
|
Ⅰ |
Ⅱ |
Ⅲ |
|
TA= uU TB= uV TC= 0 |
TA= 0 TB= uV-uU TC= -uU |
TA= uU-uV TB= 0 TC= -uV |
五段法中零矢量全部选取为000,而若要实现七段法,需要替换一半时间的零矢量为111,则只需进一步通过下式修改即可。
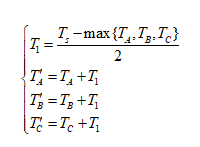
(2)
式中Ts为微机定时器周期值。可见,改进后的SVPWM算法只由乘加法与条件语句组成(小数使用Q格式运算),大大减小了运算难度,易于微机实现。
为验证改进SVPWM算法的正确性,基于MATLAB/SIMULINK环境进行仿真,算法利用M语言通过S-Function实现。为便于对比,三相占空比(比较值)与线电压均作归一化处理,结果如图4所示。
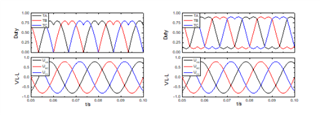
图5五段法仿真结果(左)与七段法仿真结果(右)
同时在TI C2000系列微控制器TMS320F28027上进行实物代码验证,下图为采用五段法时上桥臂AB两相的调制波形,调制波形是经过RC低通滤波的,以去除高频斩波分量,该调制波形为典型马鞍波,与仿真结果相符。利用IO电平翻转指示运算时间,在60MHz主频的F28027上(Flash运行)三扇区快速SVPWM算法(第一段高电平)只需消耗8.9us,而传统六扇区算法(第二段高电平)需要16us,可见三扇区算法可减小约44%执行时间并且代码也更为简洁(如附录)。
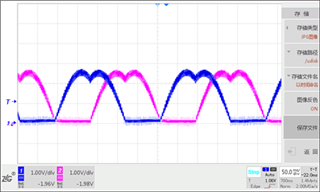
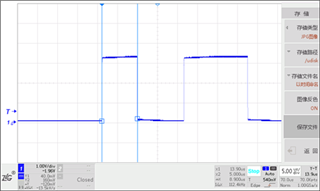
图6五段法实验结果(左)与算法消耗时间(右)
通过仿真与实验结果可见,本文提到的基于三扇区的快速SVPWM在原理上以及实际实现上都是可行的,同时简化的运算易于微机实现,适合应用在诸如各类经济型变频器等对微处理器成本敏感的场合。
五段法关键参考代码:
|
三扇区快速SVPWM |
传统六扇区SVPWM(已优化浮点与三角运算) |
|
//uA,uB分别为UV轴电压,18918为Q15下的1/square(3),37836为Q15下的2/square(3) uA=u_alpha+((18918*u_beta)>>15); uB= ((37836*u_beta)>>15);
//TA,TB,TC为三相上桥臂比较器值 if((uA>=0)&&(uB>=0)) { TA=uA; TB=uB; TC=0; }
if((uA<=0)&&(uA<=uB)) { TA=0; TB=uB-uA; TC=-uA; }
if((uB<=0)&&(uB<=uA)) { TA=uA-uB; TB=0; TC=-uB; }
|
//18918为Q15下的1/square(3),37836为Q15下的2/square(3),56754 is Q15下的 square(3) X= u_beta; Y= 56754*u_alpha-u_beta; Z= -56754*u_alpha-u_beta;
if(X>=0) { if(Y>0) { Sector=1; } else if(Y<=0) { if(Z<0) { Sector=2; } else if(Z>=0) { Sector=3; } } } else if(X<0) { if(Y<=0) { Sector=4; } else if(Y>0) { if(Z>=0) { Sector=5; } else if(Z<0) { Sector=6; } } }
switch(Sector) { case 1: U4= u_alpha-((18918*u_beta)>>15); U6= ((37836*u_beta)>>15); TA=U4+U6; TB=U6; TC=0; break; case 2: U6= u_alpha+((18918*u_beta)>>15); U2= -u_alpha+((18918*u_beta)>>15); TA=U6; TB=U2+U6; TC=0; break; case 3: U2= ((37836*u_beta)>>15); U3= -u_alpha-((18918*u_beta)>>15); TA=0; TB=U2+U3; TC=U3; break; case 4: U3= -u_alpha+((18918*u_beta)>>15); U1= -((37836*u_beta)>>15); TA=0; TB=U3; TC=U1+U3; break; case 5: U1= -u_alpha-((18918*u_beta)>>15); U5= u_alpha-((18918*u_beta)>>15); TA=U5; TB=0; TC=U1+U5; break; case 6: U5= -((37836*u_beta)>>15); U4= u_alpha +((18918*u_beta)>>15); TA=U5+U4; TB=0; TC=U5; break; } |