你(们)好
我最终设法为传递函数分配了非常需要的时间、并在2020年2月解决了我原来的文章"UC3842传递函数"
使用 Plant Transfer 函数绘制增益和相位图来解决问题的简短答案是将 "s"替换为"jw"。
这些传递函数是标准的2端口系统、其中 H =输出/输入 =数字器/分母、数字器 N 保持所有零、分母 D 保持所有极
因此、通过查看函数、我们可以清楚地看到存在多少个极点和零。
对于单极 H (s)= 1 /(1 + s/WP)的传递函数 、我们有 D (s)= 1 + s/WP、用 JW 替换"s"、我们得到 D (s)= 1 + j*W/WP。
现在我们用 sqrt (-1)替换"j"、因此我们用 D (s)= sqrt (1 +(W/WP)^2)求解
然后 H (s)= 1/sqrt (1 +(W/WP)^2)
请注意、我们使用的是"弧度而非频率"。 因此 W = 2 * PI *频率
WP = 2 * PI * FreqPole
如果我们看一下相移、我们得到 Theta =-arctan (W/WP)、因此在极点、当 W = WP 时、我们在 FCorner 处获得-45度的滞后。 这与我们从文本簿 集成器中学到的完全相同。
通过使用 H (s)= 1/sqrt (1 +(W/WP)^2)和设置 W = WP、我们得到1/sqrt (2)和20Log (1/sqrt (2))=-3dB。 这证明了极点的传递函数在 FC-3dB 时具有-45度。
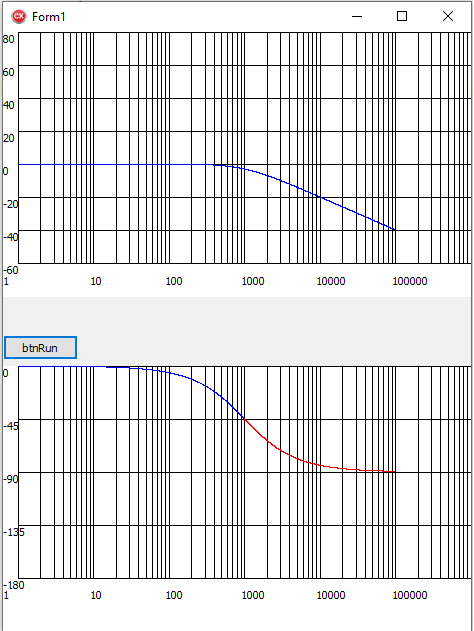
下面是 Fc = 1kHz 时的单极图。 我们可以看到、它在-3dB 时跨越1kHz、斜率为-1、相位为-45度。 在-20dB/十倍频程的情况下、我们将根据理论预期在理想的-1行中削减10kHz 和100kHz。
对于零、我们将反转该图、因此我们不会降低-1、而是使用+1和+45度的相位升压。
通过查看数学形式 (1+ s/W)、我们可以在 UC3842传输函数中找到它们、分别为极点和零点。
h (s)=GO *(1.0 +(s/Wesrz))*(1.0 -(s/Whrhpz))/(1.0 +(s / WP1)*(1 /(1.0 +(s/(WP2 * Qp)+(Power (s、2)/ Power (Wp2))))))));我们可以看到此函数的格式正确。 因此、使用与单极点相同的形式求解。
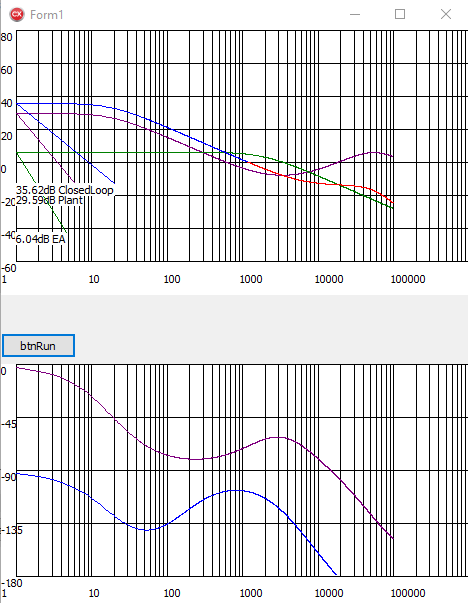
这将导致 Plant、ErrorAmp 和 Closed Loop、如下图所示。 为了绘制闭环图、我们只需将 OpenLoop 与 ErrorAmp 函数相乘。 从该图中、我们现在可以看到闭环交叉频率刚好高于1kHz、"在 ClosedLoop 增益图蓝色和红色相位相遇的点"、-1个平坦斜率和12dB GainMargin 的充足相位裕度、从而建立了一个稳定的系统。 始终使用 VNA 检查结果并在整个输入和负载范围内进行测试、通常需要调整 EA 增益以将交叉频率设置为设计的频率。
我希望这能帮助其他设计人员制作自己的波特图!! 市场上有令人惊叹的补偿器设计工具、但是编写自己的工具将使您更好地了解这个庞大而复杂的领域。
此致、保持健康、
Werner。