fft蝶形计算的每一次迭代都分为IQ两路进行运算,且输入输出位宽都是24bit,第一路经过加法器输出后的数据需要进行饱和MSB或clip LSB的操作,请问这部分的饱和截位操作有没有详细的matlab部分说明?因为我的数据都是定点数,计算过程中一旦发生饱和或截位操作就会直接影响fft计算结果,与MATLAB本身的FFT库结果对不上了o(╥﹏╥)o。
This thread has been locked.
If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.
fft蝶形计算的每一次迭代都分为IQ两路进行运算,且输入输出位宽都是24bit,第一路经过加法器输出后的数据需要进行饱和MSB或clip LSB的操作,请问这部分的饱和截位操作有没有详细的matlab部分说明?因为我的数据都是定点数,计算过程中一旦发生饱和或截位操作就会直接影响fft计算结果,与MATLAB本身的FFT库结果对不上了o(╥﹏╥)o。
我给您提供一种思路
在MATLAB中,通过一些函数来模拟定点数的饱和和截断操作。
% 定义输入数据 input_data = your_input_data; % 替换为您的输入数据 % 定义饱和边界 saturation_limit = 2^(24-1) - 1; % 24位的定点数,最高位是符号位 % 饱和操作 saturated_data = min(max(input_data, -saturation_limit), saturation_limit); % 截断操作 truncated_data = int32(input_data); % 将数据转换为32位有符号整数 truncated_data = bitshift(truncated_data, -8); % 截取前24位 % 定义输出数据 output_data = fft(saturated_data); % 使用饱和后的数据进行FFT计算 % 或者 output_data = fft(truncated_data); % 使用截断后的数据进行FFT计算
假设输入数据已经存储在 `input_data` 中。饱和操作通过 `min` 和 `max` 函数来实现,确保数据不会超出指定的范围。而截断操作通过先将数据转换为32位有符号整数,然后使用 `bitshift` 函数来实现,将数据的高位截取掉,只保留24位。
另外对于fft性能的评估标准:
我设计的fft与MATLAB fft库进行了两组256点fft对比,且只考虑饱和,未考虑截位情况,结果如下:
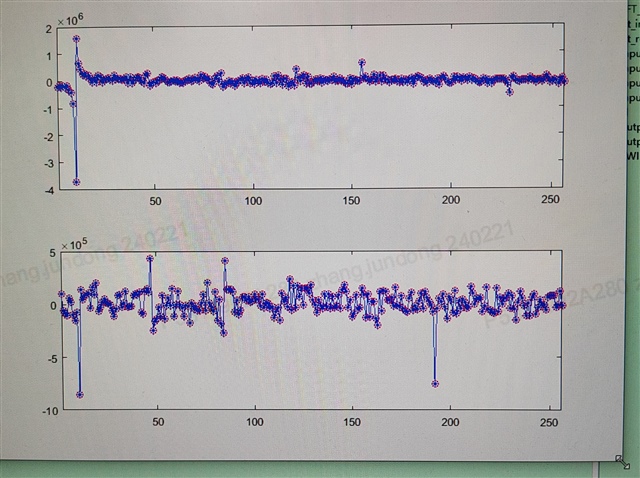
图像分别表示fft实部和虚部计算的结果,红色代表MATLAB计算的结果,蓝色表示我写得fft计算结果,此时信噪比大概在90db以上,因为此过程没发生饱和处理,所以误差较小。但是当计算过程中出现了饱和处理,计算结果见下图:
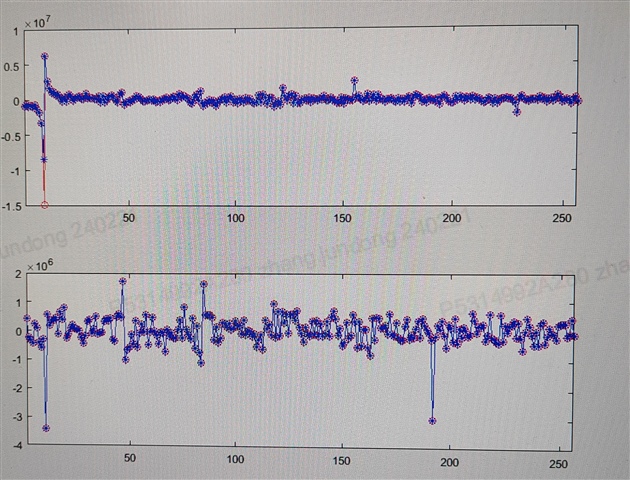
此时能看到实部结果会存在计算误差,且信噪比降到了20db,请问这种情况是否正常呢?或者这种误差有没有处理的方法?
谢谢。
对于数据类型的转换,尤其是从一个较大范围的数据类型(64位整数)转换为一个较小范围的数据类型(32位整数),会导致精度损失或数据溢出。
比如输入数据是640,那么将它转换为int32后的值还是640,
在你提到的情况中,将输入数据640转换为32位有符号整数时,确实不会发生数据变化,因为640在32位有符号整数范围内是可以表示的。但是,如果你的输入数据超出了32位有符号整数的表示范围,那么就会发生溢出。
例如,如果你的输入数据是10000000000,这个数在32位有符号整数的范围内无法表示(它超出了[-2147483648, 2147483647]的范围),这时候就会发生溢出,导致截断错误。
关于截断,当你把一个更大范围的整数转换为一个较小范围的整数时,高位的数值会被截断掉。这就意味着如果原始数据超出了目标数据类型的范围,截断后的结果可能会出现明显的误差
误差是正常的,因为饱和会引入非线性失真,导致信号的频谱发生变化,从而影响FFT计算结果
那该用什么指标来衡量设计的fft性能呢?主要还是没办法确定设计的fft能否应用。我计算信噪比的方法是将设计的fft计算结果与matlab中fft的计算结果幅值偏差作为量化噪声,得到的信噪比较小(结果图如下),请问还有没有其他更好的衡量标准呢?期待您的回复。
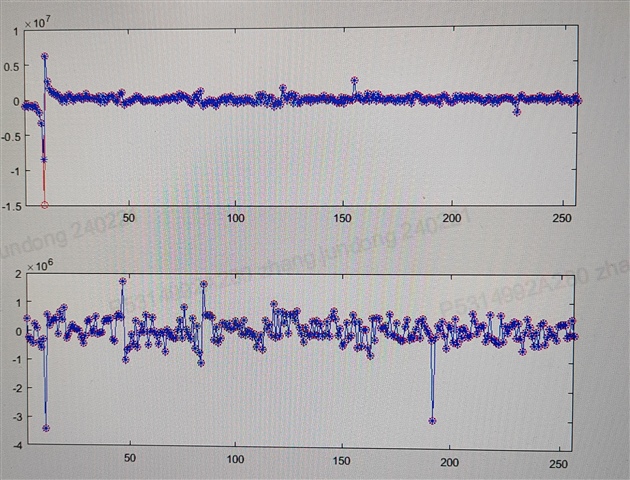
% 计算与MATLAB幅值求平均误差作为量化噪声
error_abs = mean(abs((output_matlab) - output_sim));
% 计算信噪比
db_sqnr = db(mean(abs(output_matlab))) - db(mean(error_abs));
% 计算结果
error_abs :
101340.0000351
db_sqnr :
21.9126787dB
是的
无论是饱和还是截位操作,都是针对输出数据超过范围的情况下进行的是吧?
请问还有没有其他更好的衡量标准呢
我更倾向推荐用SQNR
一种改进计算 SQNR 方法:
1. 确保计算量化噪声时准确捕捉到了输出信号与 MATLAB FFT 计算结果之间的差异
2. 计算输出信号的能量,可以用幅值的均方根 (RMS) 值来表示
3. 计算量化噪声的能量,可以用其均方根值表示
4. 计算 SQNR,即输出信号能量与量化噪声能量的比值
% 计算与MATLAB幅值求平均误差作为量化噪声
error_abs = mean(abs((output_matlab) - output_sim));
% 计算信噪比
db_sqnr = db(mean(abs(output_matlab))) - db(mean(error_abs));
% 计算结果
error_abs :
101340.0000351
db_sqnr :
21.9126787dB
% 计算输出信号与 MATLAB 幅值的均方根误差作为量化噪声 error_rms = sqrt(mean(abs(output_matlab - output_sim).^2)); % 计算输出信号的均方根值 signal_rms = sqrt(mean(abs(output_matlab).^2)); % 计算 SQNR sqnr = 20 * log10(signal_rms / error_rms);
因为我计算出的SQNR值更小了,主要是受饱和截位的影响┭┮﹏┭┮。