[参考译文] TMS320F28377S：使用128点复数 FFT 执行256点 RFFT 时出现问题

https://e2e.ti.com/support/microcontrollers/c2000-microcontrollers-group/c2000/f/c2000-microcontrollers-forum/1278890/tms320f28377s-issue-while-performing-256-points-rfft-using-128-points-complex-fft

我已使用 VCU2库成功实现了32和128点实数 FFT。  使用64点 CFFT 执行128点 RFFT。 现在我们需要将点数增加到256、所以我将处理128点复数 FFT。 我已在 RAM 中分配了一个与256对齐的输入和输出缓冲器。 具体声明如下：

//Input buffer is allocated to 256 words aligned section in RAM
#pragma DATA_SECTION(Vgrid_FFT_in_buf,"buffer1")
int16_t Vgrid_FFT_in_buf[256];
//Output buffer is allocated to 256 words aligned section in RAM
#pragma DATA_SECTION(Vgrid_FFT_out_buf,"buffer2")
int16_t Vgrid_FFT_out_buf[256];

该段在链接器文件中定义如下：

     /* Allocate twiddle factors area: */
   twiddleFactors   : > FLASHA_N,        PAGE = 0
   /*Allocate areas for 32 points RFFT input and output buffers*/
   buffer1          : > RAMLS_PROG, ALIGN = 256, PAGE = 0
   buffer2          : > RAMLS_PROG, ALIGN = 256, PAGE = 0

FFT 处理程序初始化如下：

CFFT.pInBuffer = Vgrid_FFT_in_buf;
    CFFT.pOutBuffer = Vgrid_FFT_out_buf;
    CFFT.init = (void (*)(void*)) CFFT_init128Pt;
    CFFT.run = (void (*)(void*)) CFFT_run128Pt;
    // Step 2: Initialize the handle
    handleCFFT = &CFFT;

为了测试我已经生成的代码、在一个完整周期内对以下信号进行256点采样。

X=2000+ 1000*sin (t)+700*sin (2*t)+500*sin (3*t);

采样信号存储在256长度的 uint16_t 数组中、如下所示：

uint16_t matlab_sig[256] = { 2000, 2096, 2191, 2286, 2380, 2472, 2564, 2653,
                             2741, 2826, 2909, 2989, 3066, 3139, 3210, 3277,
                             3340, 3399, 3454, 3504, 3551, 3593, 3631, 3664,
                             3693, 3717, 3736, 3751, 3762, 3768, 3770, 3767,
                             3761, 3750, 3735, 3717, 3695, 3670, 3642, 3610,
                             3576, 3539, 3500, 3458, 3415, 3370, 3324, 3276,
                             3228, 3178, 3129, 3079, 3029, 2979, 2930, 2881,
                             2833, 2786, 2740, 2696, 2653, 2612, 2573, 2535,
                             2500, 2467, 2436, 2407, 2380, 2356, 2334, 2314,
                             2297, 2282, 2270, 2259, 2251, 2245, 2240, 2238,
                             2238, 2239, 2241, 2245, 2251, 2257, 2265, 2273,
                             2282, 2292, 2302, 2312, 2322, 2332, 2342, 2352,
                             2361, 2369, 2377, 2383, 2389, 2393, 2397, 2399,
                             2399, 2398, 2396, 2392, 2387, 2380, 2371, 2361,
                             2350, 2336, 2322, 2305, 2288, 2269, 2249, 2227,
                             2205, 2182, 2157, 2132, 2107, 2080, 2054, 2027,
                             2000, 1973, 1946, 1920, 1893, 1868, 1843, 1818,
                             1795, 1773, 1751, 1731, 1712, 1695, 1678, 1664,
                             1650, 1639, 1629, 1620, 1613, 1608, 1604, 1602,
                             1601, 1601, 1603, 1607, 1611, 1617, 1623, 1631,
                             1639, 1648, 1658, 1668, 1678, 1688, 1698, 1708,
                             1718, 1727, 1735, 1743, 1749, 1755, 1759, 1761,
                             1762, 1762, 1760, 1755, 1749, 1741, 1730, 1718,
                             1703, 1686, 1666, 1644, 1620, 1593, 1564, 1533,
                             1500, 1465, 1427, 1388, 1347, 1304, 1260, 1214,
                             1167, 1119, 1070, 1021, 971, 921, 871, 822, 772,
                             724, 676, 630, 585, 542, 500, 461, 424, 390, 358,
                             330, 305, 283, 265, 250, 239, 233, 230, 232, 238,
                             249, 264, 283, 307, 336, 369, 407, 449, 496, 546,
                             601, 660, 723, 790, 861, 934, 1011, 1091, 1174,
                             1259, 1347, 1436, 1528, 1620, 1714, 1809, 1904 };

因此、直流分量为2000、第一谐波为1000、第二谐波为700、第三谐波为500 Vpk。

以下是用于执行实际 FFT 的函数。

static inline void calculate_THD(void)
{
    uint16_t i, j;
    float32_t THD;

    //NOTE:Consider using memcpy
    for (i = 0; i < 256; i++)
    {
        Vgrid_FFT_in_buf[i] = matlab_sig[i];
    }
    //running FFT on grid voltage samples
    CFFT.run(handleCFFT);
    //Unpacking is required as 128 point real FFT is performed using 64 points complex FFT.
    CFFT_unpack(handleCFFT);
    //Post processing FFT results

    magFFT[0] = CFFT.pOutBuffer[0] * 0.0313 * 5;
    //Calculating magnitude till 7th harmonic
    for (i = 1; i < 8; i++)
    {
        j = 2 * i;
        magFFT[i] =
        sqrtf(((float) CFFT.pOutBuffer[j] * (float) CFFT.pOutBuffer[j])
                + ((float) CFFT.pOutBuffer[j + 1]
                        * (float) CFFT.pOutBuffer[j + 1]));
        //scaling factor is (1/2^12)/Vgrid1_gain = 0.0313
        //furthermore the library scales the ouput result by N where 2^N = # of samples. for 32 samples N=5.
        //since we are measuring a single phase so we scale by 2 to measure line to line voltages.
        magFFT[i] = magFFT[i] * 0.02901 * 5 * 2; //0.0313 prev gain

    }

    THD = 0.0f;
    for (i = 2; i < 8; i++)
    {
        THD = magFFT[i] * magFFT[i] + THD;
    }
    THD = sqrtf(THD);
    //Updating array of harmonics effective values
    //Shifting all values one left. Discrading the oldest value.
    for (i = 15; i > 0; i--)
    {
        harm_eff_values[i] = harm_eff_values[i - 1];
    }
    harm_eff_values[0] = THD;
    //Updating array of fundamental values
    for (i = 5; i > 0; i--)
    {
        fundamental_values[i] = fundamental_values[i - 1];
    }
    fundamental_values[0] = magFFT[1];
    fft_updated = true;

}

现在来看看问题：对该函数的首次调用给出了正确的结果、但下一次调用给出了错误的结果、并且这对于所有连续调用(即、一次调用给出了正确的结果、而下一次调用给出了错误的结果)继续。

请在下方查看从调试的观察窗口捕获的结果：

校正结果：

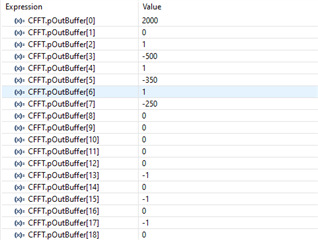
错误结果：

请注意、我每5秒调用一次函数、以便监视窗口有足够的时间进行刷新。 我一直在尝试解决它我自己,但到目前为止没有成功。 我使用的是 C2000Ware 4.0.2、编译器版本是 22.6.0.LTS。 如果需要更多信息、请告诉我。