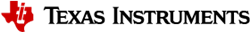LP5036为 LEDx_Brightness 寄存器提供了对数刻度调光选项、数据表第14页对此进行了介绍。 图11的右侧图显示了一条传输曲线:

我想知道使用了什么电光传递函数(EOTF)来生成该曲线。 它与 sRGB EOTF (线性拐点、后跟2.4伽马指数)不匹配、也不匹配简化的2.2伽马指数型号。 我尝试了 ax^b 和 b^(x-1)形式的回归,使用了三个最明确的点--[0,0],[160/255,0.2],[1,1]但这些拟合都没有产生与图匹配的曲线。
我还想澄清一下量化在线性工作模式与对数工作模式下的影响。 这有点复杂、因此一些背景按顺序显示:
当以线性模式运行时、8位值映射到 LED 的线性(非感知)亮度。 但是、每个阶跃的感知亮度增量不是恒定的、因为我们的眼睛对更暗光中的亮度变化比更亮的光中的亮度变化更加敏感、即从1到2的阶跃比从251到252的阶跃更加明显的感知亮度变化。 伽马校正旨在通过线性和感知空间之间的映射来解决这一问题。 然而、如果在软件中执行伽马校正并且硬件仍通过一个8位量化线性亮度值进行控制(通过 EOTF 从感知空间转换)、这将导致较低亮度值被显著破坏、从而产生步进和条带。 虽然可以增加位深度以缓解该问题(在驱动器 TR/TF 要求方面进行权衡)、但理想解决方案是使硬件在感知空间中接受量化值并利用恒定电流或 PWM 控制环路的非量化(或更高的位深度量化)调整。 这会导致每个量化值步长(0到1、1到2、... 254到255)产生感知的恒定亮度变化、从而消除了破碎和条带问题。 推测这是 LP5036中的对数调光曲线模式的目的。
数据表指出:"如果需要特殊的调光曲线、使用带软件校正的线性标度是最灵活的方法"。 线性模式确实使在软件中实现任意 EOTF 而不使用硬件对数曲线变得很琐碎、但为简单起见、您需要权衡一下对数模式要解决的问题。 在我看来、如果我想要一个更好的结果、我应该定义一些函数、将感知亮度转换为 LP5036的硬件特定对数亮度空间。 例如、如果硬件的 EOTF 为 H (x)= x^3.0、而我的目标 EOTF 为 E (x)= x^ 2.2、那么我可以将 E'(x)= x^(2.2/3.0)定义为一个中间转换函数、这样 H (E'(x)= x^2.2。
我在图形计算器中对此进行了测试: https://www.desmos.com/calculator/ismfjbchot

蓝线代表执行软件伽马校正然后在线性空间中量化的典型方法。 您可以在低端看到显著的步进、最小非黑色感知亮度约为8%、产生的对比度仅为12.5、这非常差。
绿线表示创建中间函数的替代方法、该函数用于从所需的 EOTF 映射到硬件的 EOTF、然后在硬件的非线性亮度空间中量化。 这在步长上仍然会产生学不到的感觉、但有好处是使步长在低亮度区域小得多。 对于硬件内部传输曲线近似指数大于1的所有情况、这会产生改进的结果。 权衡是在高亮度区域中增加量化误差、但感知误差的总体幅度要低得多(对于典型指数低至三分之一)。
但是、只有当中间伽马空间中的8位量化是唯一在硬件内应用的量化时、这种改进性能的假设才有效。 如果硬件使用 LUT 简单地从8位"日志"空间转换回8位线性空间、以便感知值的第一个~8%在实践中映射到零亮度、则无论如何都会出现粉碎效果。 如果硬件使用 LUT 将8位"日志"空间转换为更高的位深度(例如10位或12位)线性空间、则中间伽马转换方法的效果应该保持不变、但需要进一步描述。 这是我希望更好地理解的内容。
LP5036的"对数"传递曲线是如何在线性量化方面实现的? 曲线 LUT 是否会(在对数空间中)将8位量化输入值直接映射到线性空间中的12位值、该值又分为9位 PWM 深度和3位时间抖动深度?