Other Parts Discussed in Thread: C2000WARE,
C2000Ware版本:5.02.00.00
DCL(Digital Control Library)版本:3.4
常用的PID控制器通常为线性PID控制器,即各控制环节将产生的偏差信号(给定信号rk-反馈信号yk)与常数相乘(比例系数、积分系数、微分系数),因此其计算过程为线性运算过程。
实际应用过程中,对于偏差信号也可以采用非线性的方式进行处理,以进一步改善线性PID的动态响应特性,此种PID控制器成为非线性PID控制器。
本文由以下三部分组成:
原理讲解
代码移植
调试
1.原理讲解
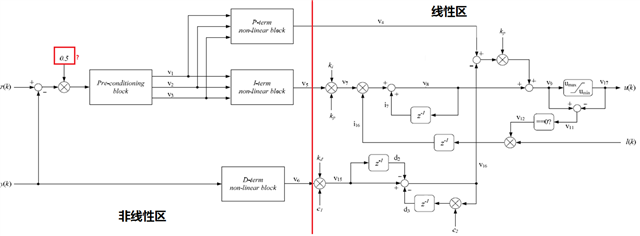
图1. DCL_NLPID_C2/C3结构
如图1所示,为C2、C3类型非线性PID控制器结构图。非线性PID控制器可以分为线性区和非线性区两部分,线性区为常规的串行结构PID控制器,非线性区对偏差信号进行非线性处理。DCL_NLPID_C2/C3控制器源码位于以下路径:
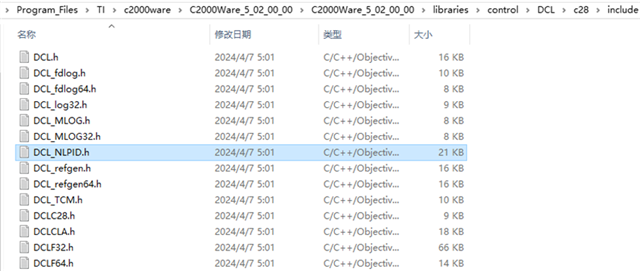
图2. DCL_NLPID.h文件路径
DCL中的功能全部由可编辑代码构成,不依赖其它库文件,允许用户进行修改,这一点还是很方便的。在本文后续的调试过程中,笔者认为非线性区将偏差信号乘以0.5是不合理的,因此对DCL_NLPID_C2源码做了变更,注释掉了0.5系数,如下图所示:

图3. DCL_NLPID_C2非线性区代码变更
在图3中,左侧为原始代码,右侧为变更后的代码。
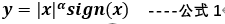
在公式1中,X为偏差信号(rk-yk),非线性区的工作原理为对偏差信号进行幂函数运算,得到如下曲线:
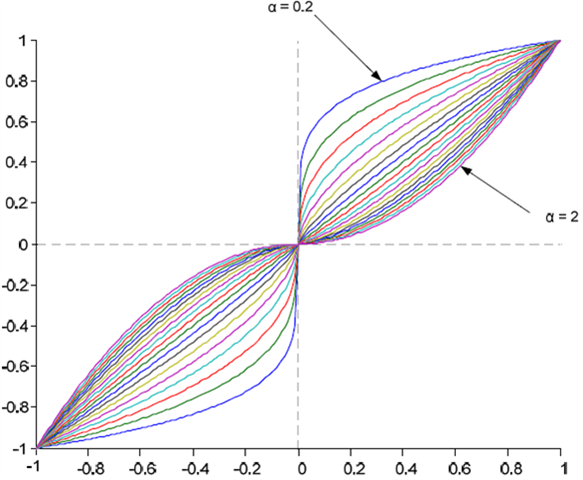
图4. 非线性区曲线
在图4所示的曲线中,X轴为偏差信号,Y轴为非线性区输出信号,X的范围为±1,该图绘制了α = 0.2至α = 2的典型曲线。当α = 1.0时,非线性PID表现为线性PID;当α 1时,在幂函数的作用下,偏差呈现出增大或变化加剧的特点;当α 1时,在幂函数的作用下,偏差呈现出减小或变化迟缓的特点。
需要注意的是X接近0(偏差接近0)即系统接近稳态时,以图4中α = 2曲线为例,X越接近0,经幂函数运算后的系统偏差越小,这意味着系统需要更长的时间进入稳态,或者经过多次震荡后进入稳态,达到稳态后控制器对扰动的响应变得迟缓;当α = 0.2时,X越接近0,经幂函数运算后的系统偏差越大,这意味着控制器对偏差的调节作用加强,系统会相对较快地进入稳态,达到稳态后控制器对扰动响应变得敏感,可能出现震荡。
为了解决以上问题,我们需要在X等于0附近设置线性区,对该区域内的偏差依然进行线性运算调节,将公式1做如下调整:
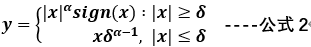
在公式2中,线性区范围大小由delta决定,线性区斜率称为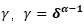 , 公式2对应的曲线为:
, 公式2对应的曲线为:
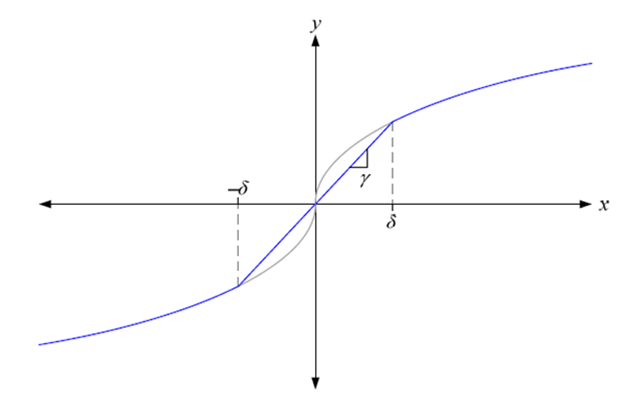
图5. 公式2曲线
2.代码移植
在DCL中, 有3种FPU32类型的非线性PID控制器,其执行函数分别为DCL_runNLPID_C1、DCL_runNLPID_C2和DCL_runNLPID_C3。DCL_runNLPID_C1为并行结构的非线性PID控制器,DCL_runNLPID_C2为串行结构的非线性PID控制器,DCL_runNLPID_C3为需要TMU-Type1支持的串行结构非线性PID控制器。DCL_runNLPID_C1和DCL_runNLPID_C2的定义位于DCL_NLPID.h文件,DCL_runNLPID_C3由汇编语言实现,位于以下路径:
\C2000Ware_5_02_00_00\libraries\control\DCL\c28\source\ DCL_NLPID_C3.ASM
我们使用DCL_runNLPID_C2型非线性PID控制器。
DCL中的非线性PID控制器有比较安全的操作机制,如错误检查、参数更新等。
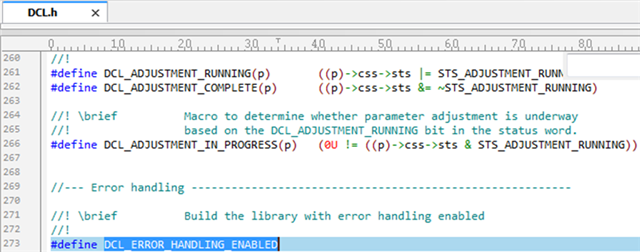
图6. 错误检查宏定义
如图6所示,DCL.h文件中定义了错误检查宏,
将位于\C2000Ware_5_02_00_00\libraries\control\DCL\c28\source路径下的DCL_error.c文件添加到工程中,当控制器执行过程中发生错误时,系统会调用DCL_error.c文件中的DCL_runErrorHandler函数终止程序执行并报告错误原因,这对调试阶段很有帮助。
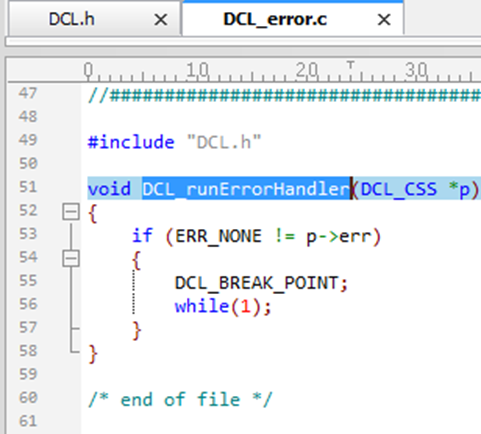
图7. DCL_runErrorHandler函数定义
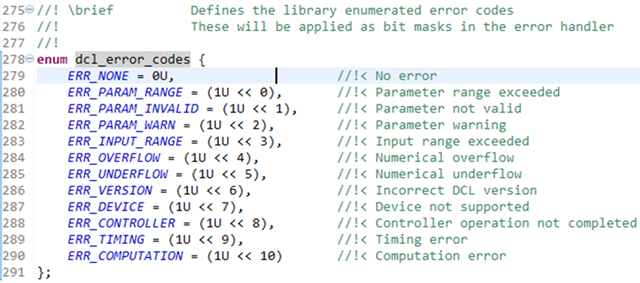
图8. Error Code定义
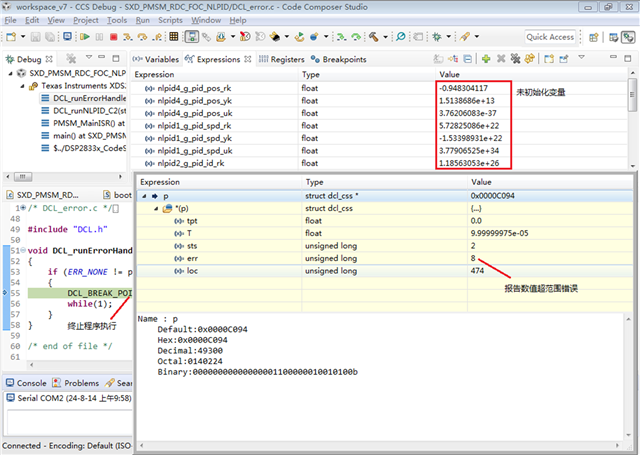
图9. 控制器执行错误举例
如图9所示,笔者在调试时定义了一些未初始化变量,这些变量用于在程序执行过程中存储控制器相关数值,如控制器输出、控制器反馈输入以及控制器参考输入等。由于这些未经初始化的变量被随机赋予了一些比较大的随即数值,因此系统报告了错误代号8即输入超范围错误。
对于控制器参数更新,DCL允许用户选择性地使用SPS(Shadow Parameter Set),不过这里还是建议大家使用SPS。
如果需要改变控制器参数,不是使更新立即生效,新的控制器参数将被写入到结构体SPS相关变量中,在用户申请更新控制器参数并调用更新函数后,新的参数才被写入到控制器中并生效。
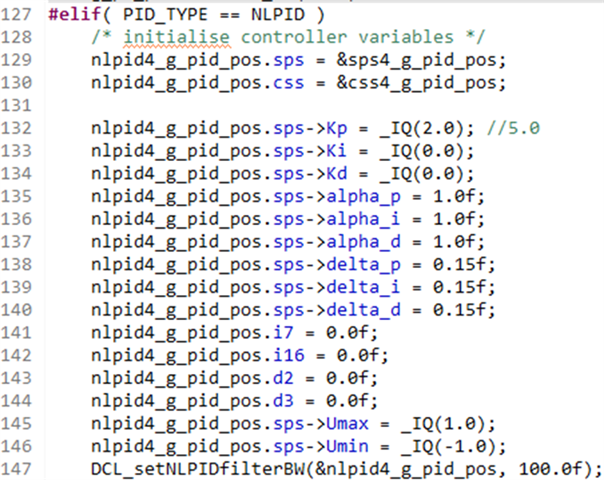
图10. 位置环非线性PID控制器参数初始化举例

图11. 位置环非线性PID控制器参数更新举例
控制器参数更新函数将关闭系统中断进行参数更新,即将SPS中的参数复制到Active变量中,完成后再打开系统中断,这避免了在算法执行过程中更新控制参数带来的未知风险,使得控制参数更新更加安全。对于实时性要求比较高的应用场景,DCL也提供了汇编语言编写的参数快速更新函数供用户使用。
DCL_runNLPID_C2型非线性PID控制器使用了POW函数,即幂函数,该函数运行会占用比较多的系统时间,笔者调试使用的C2000系列控制器是TMS320F28335,其On-Chip ROM的FPU math tables中不支持POW函数运算。
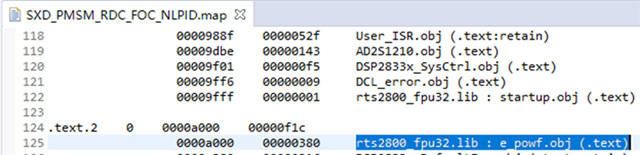
图12. map文件中的pow函数
如图12所示,pow函数使用的是运行支持库rts2800_fpu32.lib中的函数,

即e_powf.c文件中的float powf(float x, float y)函数。使用非线性PID控制器时,需要注意幂函数运算时间对算法控制周期产生的影响。
在C2000系列处理中执行POW函数运算有3种方式,第一种方式就是本文使用的运行支持库rts2800_fpu32中的相关函数,一次幂函数运算将消耗上百个CPU时间,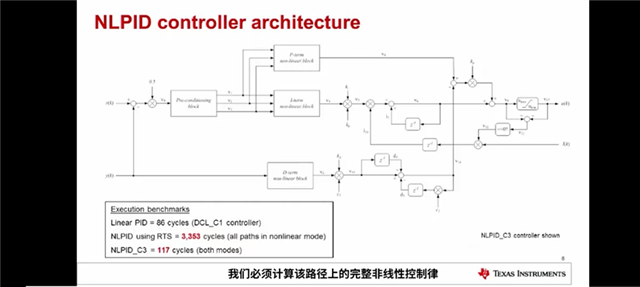
图13. Pow函数运行时间
如图13所示,使用RTS库(rts2800_fpu32),如果所有控制环节都工作在非线性区,将耗时3353个CPU时间,以150MHz主屏计算,3353 * 6.67nS = 22.36uS,这是时间大家可以做个参考。
第二种方式是使用fastFPU中经过优化但运算精度有些损失的幂函数,如下图所示:

图14. fastFPU中的pow函数
如图14所示,pow函数的执行耗时109个CPU时间。
执行效率最高的是在配备了TMU-Type1的处理器上执行幂函数运算,如下图所示:

图15. 幂函数运算数学等效变换及TMU-Type1新指令
在图15中,对幂函数做了数学上的等效变换,变换后的运算由以2为底的log运算和2的幂函数运算两种运算构成,TMU-Type1中添加了对这两种运算的支持,这使得等效变换后的幂函数运算时间大幅缩减,具有TMU-Type1的C2000系列控制器如280025、28P65等,是该系列相对较新的处理器,DCL_runNLPID_C3就是在这类处理器上运行的非线性PID控制器。
设计位置环非线性PID控制器时,对于偏差同样需要做“roll in the error”处理,而不是直接使用DCL库中的DCL_runNLPID_C2型非线性PID控制器。否则当电机运行至设定位置0时将失控或者跑飞。为此笔者在DCL_NLPID.h文件中增加了DCL_runNLPID_C2_POS函数,该函数与DCL_runNLPID_C2函数的不同之处如下图所示:
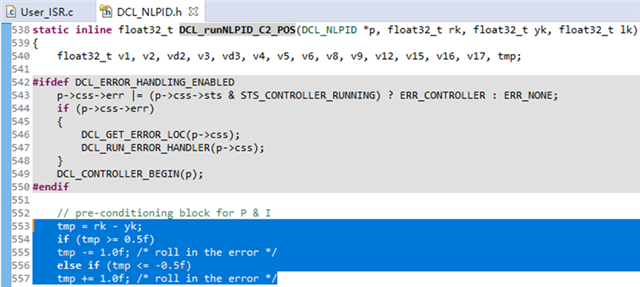
图16. DCL_runNLPID_C2_POS的roll in the error处理
3.调试
控制器:TMS320F28335
电机类型:PMSM
位置反馈单元:旋转变压器
控制算法:FOC,位置+速度+电流三闭环控制
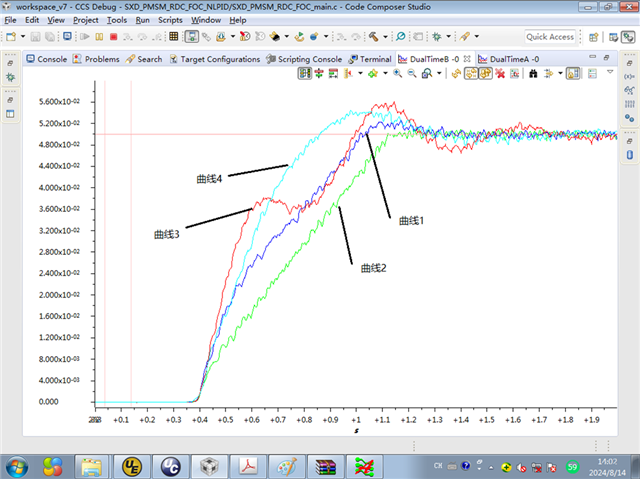
图17. 实验曲线
图17为转速+电流双闭环模式下利用DCL_TCM功能截取的启动波形,X轴为时间,Y轴为归一化转速数值,测试时设定转速0.05,对应电机实际转速为375RPM。
曲线1(深蓝色)是将非线性PID控制器各环节的α参数设置为1.0,即使非线性PID控制器表现为线性PID控制器得到的启动波形;
曲线2(绿色)是将速度环比例环节的α参数设置为0.5得到的启动波形,当α小于1时,幂函数将偏差放大,因此系统较快地达到了稳态;
曲线3(红色)是将速度环比例环节的α参数设置为1.5得到的启动波形,当α大于1时,幂函数将偏差缩小,因此系统经过较长的时间达到稳态;
曲线4(浅蓝色)是将速度环比例环节的α参数设置为1.4、积分环节的α参数设置为1.3得到的启动波形。
通过对比可以发现,在不改变比例、积分、微分系数的情况下,仅改变α,就可以改变系统动态响应特性,再配合线性区参数修改,使用非线性PID控制器会得到比线性PID控制器更好的系统动态响应特性。
结论:
本文从原理分析、代码移植、调试三方面介绍了非线性PID控制器,将α参数设置为1.0,非线性PID控制器就成为了线性PID控制器,因此在软件设计时可以直接在系统中使用非线性PID控制器,并将α参数设置为1.0进行调试,在难以满足控制要求时,可以引入非线性部分进一步改善系统动态响应特性。
笔者调试时对于偏差没有乘以0.5系数,对于位置环控制,新建立了DCL_runNLPID_C2_POS函数,大家在使用非线性PID控制器时,要注意其执行时间。